Als u regelmatig naar planten om u heen kijkt, zult u merken dat er ondanks de "chaos" in de natuur er ook veel regelmaat is. In dit artikel wil ik aandacht schenken aan die regelmaat in de natuur. Dat er een bepaalde regelmaat in patronen in de natuur op te merken valt, was al in de Middeleeuwen opgevallen. De wiskundige Fibonacci (zijn werkelijke naam was waarschijnlijk Leonardo Pisano) uit Pisa schreef in 1202 in zijn boek 'Liber Abbaci', dat de toename van konijnen (als ze niet opgegeten worden door roofdieren) verloopt volgens de reeks:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, enz.

Het plaatje van figuur 1 geeft deze reeks weer.

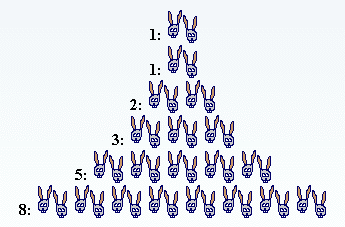Figuur 1. Een illustratie van de toename van konijnen (van de wiskunde homepage van Willem van Ravenstein)

Rond 1870 werd door de wiskundige Lucas deze reeks naar zijn ontdekker 'de reeks van Fibonacci' genoemd. Deze reeks en de afleiding daarvan, de gulden snede, blijkt in de natuur vaak voor te komen. Overigens is Fibonacci voor de Westerse beschaving tevens erg belangrijk geweest door de invoer van de Arabische cijfers (0 t/m 9), het tientallige positiestelsel en het bijbehorende rekenwerk (afkomstig van het Indische subcontinent). Hij heeft er voor gezorgd, dat we tegenwoordig gemakkelijk ingewikkelde getallen kunnen optellen, aftrekken en vermenigvuldigen. Dat was met de Latijnse cijfers I, V, X, C en M geen eenvoudige zaak.

Heeft u al ontdekt, hoe we aan het volgende getal in de reeks komen? Elk nieuw getal ontstaat, door de laatste twee getallen uit de reeks bij elkaar op te tellen.

Bij de opbouw van bloemen in onderdelen (bijvoorbeeld de kroonblaadjes) vinden we aantallen, die overeenkomen met de getallen uit de reeks van Fibonacci. Ik geef u hierbij enkele voorbeelden van het aantal bloemkroonbladeren, waaruit een bloem is opgebouwd:

• lelie en iris met 3 (de bloem bestaat wel uit 6 blaadjes, maar 3 ervan zijn kelkblaadjes)
• boterbloem en wilde roos met 5
• ridderspoor met 8
• kruiskruis met 13
• aster met 21
• weegbree met 34
• verschillende andere soorten uit de Asterfamilie met 55 of 89

Bij sommige planten is er binnen de soort variatie in het aantal bloemkroonbladeren, zodat de aantallen niet altijd precies gelijk aan zo'n getal uit de reeks. Maar als je dan naar het gemiddelde kijkt, dan is dat vaak weer een Fibonacci- getal.

Ook bij bloeiwijzen en vruchten vinden we de reeks van Fibonacci terug. Heeft u wel eens naar de bloemetjes in een grote Zonnebloem gekeken? De kleine bloemetjes lijken in spiralen gerangschikt te zijn. Je kunt één spiraal naar rechts volgen, maar ook één naar links. Tel je het aantal spiralen die naar rechts buigen en tel je diegene, die naar links buigen, dan kom je op verschillende aantallen uit. De twee getallen, die je vindt, blijken getallen uit de reeks van Fibonacci te zijn!. Hetzelfde vinden we bij de zaden in een vrucht. Een mooi voorbeeld, waarbij men de aanwezigheid van twee verschillende waarden voor het aantal spiralen kan nagaan, zijn de dekschubben van naaldboomkegels, bijvoorbeeld een dennenappel. Volg de spiralen naar links en rechts en tel het aantal. Een ander mooi voorbeeld zijn de spiralen gevormd door de zaadjes in een rijpe zonnebloem (figuur 2).

Hoe komt het dat de natuur steeds getallen oplevert, die behoren tot deze reeks? Voor een belangrijk deel zijn het ook 'onze ogen' die meewerken. Wij zien in de opeenpakking van al die bloemetjes, zaadjes of schubben mooie spiralen, maar eigenlijk is het niet meer dan een zo'n efficiënt mogelijk gebruikmaken van een cirkelvormige ruimte met daarin gelijke ronde objecten. Probeert u maar eens zo veel mogelijk even grote knikkers in een cirkelvormige ruimte te proppen.

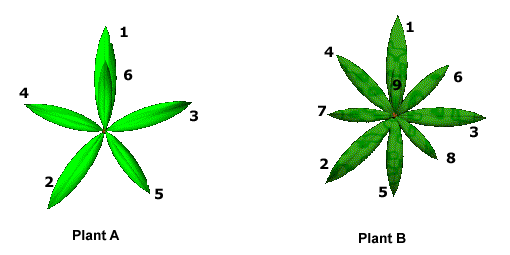
De reeks van Fibonacci wordt nog belangrijker, als we kijken naar de Phyllotaxis. De phyllotaxis is de wetenschap die zich bezighoudt met de rangschikking van bladeren langs een stengel. Bij ongeveer 90 % van de planten groeien de bladeren in een spiraal langs de stengel. In figuur 3 ziet u twee voorbeelden van planten met verschillende bladstanden.

Bij plant A moeten we, als we kloksgewijs ronddraaien, 3 rondjes maken om bij een blad te komen dat weer boven de vorige staat. Tijdens die drie rondjes passeren we 5 bladeren. Draaien we tegen de klok in, dan moeten we 2 rondjes maken. De getallen 2, 3 en 5 zijn opeenvolgende getallen uit de reeks van Fibonacci. Omdat bij dit voorbeeld kleine getallen optreden, zou men kunnen zeggen dat dit een toeval is. Maar er zijn  ook planten te vinden, die de bladrangschikking volgens voorbeeld B hebben. Bij deze plant moet u 5 rondjes (met de klok mee) of 3 rondjes (tegen de klok in) draaien om een blad te vinden, dat weer boven een ander blad staat. Als u dat doet, passeert u 8 bladeren. Ook hier vindt u drie opeenvolgende getallen uit de reeks. De bladrangschikking volgens voorbeeld A vindt u onder andere bij de eik, de kers en de appel. Die van voorbeeld B bij de populier, roos en de peer. Bij de wilg en de amandel komt de bladrangschikking overeen met de getallen 5 (tegen de klok in), 8 (met de klok mee) en 13 (het aantal bladeren tussen twee boven elkaar staande bladeren).

Waardoor ontstaan deze spiralen en wat is hun functie? Bij planten vindt de groei plaats in groeipunten. Deze groeipunten bestaan uit meristemen, weefsels waarin de cellen vaak delen. Het stengelgroeipuntje en het wortelgroeipuntje zijn voorbeelden van meristemen. Bij de vorming van cellen naar beneden toe, "draait" het stengelgroeipuntje spiraalsgewijs rond. Sommige cellen, die naar beneden gevormd worden, behouden hun delingsactiviteit. Deze cellen gaan de groeipunten voor de bladeren vormen. De bladgroeipunten ontstaan op regelmatige afstand van elkaar. Hoe die regelmaat precies ontstaat is nog niet bekend. Elk volgend blad wordt in een vaste hoek ten opzichte van het vorige blad gevormd. Omdat het stengelgroeipuntje spiraalsgewijs naar beneden cellen vormt, ontstaan er spiralen van bladeren. Deze wijze van groeien zorgt voor een optimale verspreiding van bladeren rondom de stengel: elk blad heef een grote kans om licht op te vangen en van het blad afdruppend water komt snel op de grond terecht.

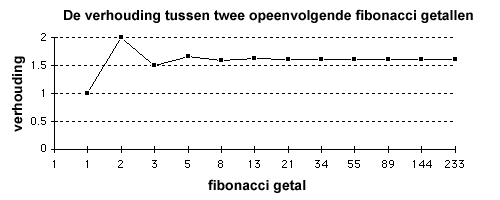
Voordat we naar die vaste hoek gaan kijken, wil ik u eerst laten zien hoe we met de getallen van de reeks van Fibonacci verder kunnen 'spelen'. Laten we elk getal uit de reeks eens delen door het vorige getal uit de reeks. We krijgen dan de volgende serie:

(1/1)= 1 , (2/1) = 2, (3/2)= 1,5 , (5/3) = 1,666..,  (8/5) = 1,6 , (13/8) = 1,6225

In figuur 4 ziet u, hoe deze verhouding tussen een getal en zijn "vorige" getal uit de reeks zich ontwikkelt.

Zoals u kunt zien, tendeert de verhouding tussen twee Fibonacci getallen naar een bepaalde waarde, die wiskundigen het getal j (phi) noemen. Het getal phi wordt ook wel het gouden getal genoemd. Evenals het getal p (pi) kan de waarde van j niet exact weergegeven worden met decimalen. Het is een irrationeel getal. Bij benadering komt het getal phi overeen met 1,618034. De verhouding van 1 : 1,618034 is ook bekend geworden onder de naam 'gulden snede'

Waarom blijkt de natuur te 'kiezen' voor de verhoudingen volgens het getal phi en pi en volgt de natuur geen andere vorm voor dichte en efficiënte stapeling? We zullen het voorbeeld uitwerken met de zaden. De meeste plantenzaden zijn rond. Als we die zaden in een omhulsel. een vrucht, willen verpakken, dan zal de dichtste pakking worden verkregen door een zogenoemde hexagonale stapeling. Maar in de natuur wordt dit niet gevolgd en volgt de zaadrangschikking het patroon naar het model van Fibonacci. Als men een hexagonale stapeling bekijkt, moeten we dat vergelijken met de stapeling van blikken in een kartonnen door. De blikken staan in rijen naast elkaar, zodat de volgende rij weer in de holten van de voorgaande geplaatst kan worden. Elk blik wordt steeds omgeven door zes andere blikken. Een stapeling van zaden zal in een dergelijke rangschikking nooit kunnen groeien. Wanneer dat wel het geval is, zal bij onregelmatige groei het ene zaad het andere verdrukken of, erger nog, bij gelijkmatige groei zullen alle zaden elkaar verdrukken. Zaden worden in een hexagonale stapeling dus niet optimaal gevormd. In een stapeling volgens het model van Fibonacci, waarbij elk zaad dus phi gedraaid ten opzichte van het voorgaande zaad groeit, zal geen enkel zaad het andere verdringen en dus ongehinderd in omvang kunnen toenemen.

We gaan weer kijken naar de vaste hoek bij de vorming van bladgroeipunten. De wiskundigen Douady en Couder hebben in 1993 bewezen, dat een vaste hoek tussen 2 groeipunten een optimale spreiding van bladeren/zaden/bloemen kan verzorgen als deze objecten naar buiten groeien. Deze hoek blijkt vaak 222,492 ° te zijn. We kunnen ook zeggen, dat de hoek 360 °- 222,492 ° = 137,508 ° is. Als we 222,492 delen door 360, dan komen we uit op 0,618034, dat is de decimale fractie van het gouden getal. Deze hoek van 222,492 ° blijkt een ideale hoek te zijn voor de rangschikking van bladeren rondom een stengel. Met rationele getallen, zoals 0,5 of 0,6, zouden de bladeren  boven elkaar komen te staan. Ook bij getallen als 0,42 0f 0,67 blijkt de ordening van bladeren over de ruimte niet optimaal te zijn. Op de homepage van R. Knott kunt u animaties bekijken van de vorming van groeipunten bij verschillende hoeken. Het rationele antwoord op de vraag hoe een ideale spreiding in de ruimte is te verkrijgen, blijkt het gebruik van een irrationeel getal te zijn! En de rationele benadering van dit irrationele getal bestaat uit de gehele getallen uit de reeks van Fibonacci

Overigens wordt het belang van de gulden snede, het gouden getal en de reeks van Fibonacci in de natuur en de kunst door sommige hedendaagse filosofen gerelativeerd. Dat doet bijvoorbeeld Albert van der Schoot, die werkzaam is in het vakgebied van de filosofische esthetica. Hoewel rond 300 voor Christus verwijzingen naar de gulden snede bij Euclides worden gevonden, blijkt het gebruik hiervan in andere wetenschappen dan de wiskunde pas vanaf de Romantiek. Dan wordt de 'goddelijke verhouding' populair. Volgens van der Schoot zijn bijna alle manifestaties van deze goddelijke verhouding in de natuur ontstaan in de menselijke geest: niet de natuur heeft die orde, maar de mens 'ziet' die orde. Maar hij maakt een uitzondering voor de phyllotaxis.

Kijkt u maar in de natuur of in de tuin en kassen van de Hortus. U zult diverse patronen van Fibonacci herkennen en versteld staat over de consistentie van vormen zoals beschreven in dit artikel. Anderzijds zijn er rangschikkingen, zoals tegenoverstaande of kransstandige bladzetting waarop het model niet werkt. De phyllotaxis is dus terecht een uitzondering op de regel.

Albert van der Schoot
De ontstelling van Pythagoras- over de geschiedenis van de goddelijke proportie
Kok Agora, 1999

Ian Stewart
Het Magisch Labyrint - de wereld bezien door wiskundige ogen
Weidenfeld & Nicholson, London. 1997

Er is veel informatie over dit onderwerp te vinden op het internet. Daarom geef ik hieronder een aantal homepages, waaruit geput is bij het schrijven van dit verhaal. Met name de eerstgenoemde website kan ik u zeer aanbevelen. Terecht heeft deze website een aantal onderscheidingen gekregen voor zijn grote educatieve waarde.

Dr Ron Knott
Fibonacci Numbers, the Golden Section and the Golden String
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html

Phyllotaxis
An Interactive Site for the Mathematical Study of Plant Pattern Formation
http://www.math.smith.edu/~phyllo/

De ontstelling van Pythagoras
Boekbespreking door Ger Groot van het boek van Albert van der Schoot
http://www.nvvw.nl/ontpyth.htm

De wiskundehomepage van Willem van Ravenstein
http://skyline.www.cistron.nl/frame.htm?url=wiskunde/